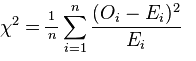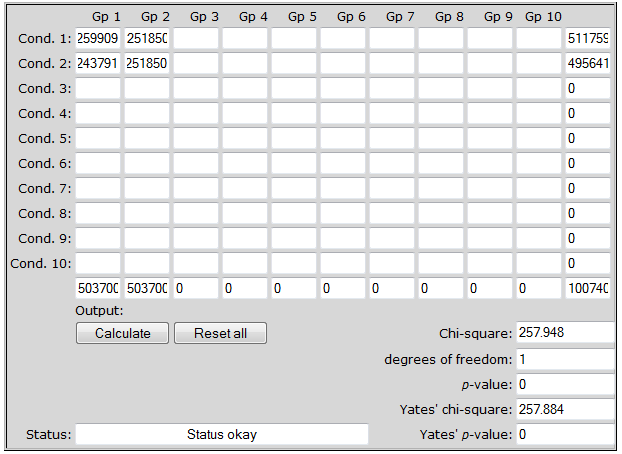
Порівняння номінальних даних

Номінальні дані організовані найбільш просто - вони являють собою певні категорії, до яких належить певна кількість об'єктів. З метою порівняння, ця кількість переводиться у частоти - відсоткову форму. Здавалося б, найлегше, що ми можемо зробити для порівняння таких даних - прямо порівняти відповідні відсотки. Проте, в багатьох випадках, особливо, при малих обсягах вибірок, таке порівняння може ввести нас в оману

У популярному науковому блозі детально розібрано, які помилки, в тому числі і статистичні, зроблені авторами однієї з статей, в якій "доводиться" шкода ГМО (обговорювана стаття була відізвана редакцією журналу саме через недостовірність зроблених висновків). Зокрема автори статті наводять дані, що у контрольній групі щурів смертність становила 30% і 20% серед самців і самок відповідно, натомість, у тварин, що вживали їжу з ГМО, цей показник становив 50% та 70%. На перший погляд цифри вражають, але прочитавши методику дослідження стає зрозумілим, що аналізувалися групи по 10 тварин, отже кожен піддослідний щур становив аж 10% від вибірки. Застосувавши статистичний метод порівняння, ми виявимо, що навіть різниця між групами самок (20% і 70%) не є статично значущою.

Отже, навіть для таких простих даних як відсотки також потрібно застосовувати статистичні методи.

Інколи ми очікуємо, що у відповідності з теорією об'єкти повинні бути розподіленими по категоріях певним чином. Наприклад, знаючи хромосомну теорію визначення статі у людини, ми можемо очікувати, що кількість народжуваних хлопчиків і дівчаток повинна співвідноситися як 1:1. Державне статистичне спостереження зазначає, що у 2013 році в Україні народилося 503700 немовлят, тобто у відповідності з нашим припущенням кількість дітей кожної статі має становити 251850. Натомість, реальні дані свідчать про переважання хлопчиків: в той рік їх народилося 259909, на відміну від дівчаток, яких було 243791. Постає питання, чи відхилення в бік народження хлопчиків є випадковим або ж обумовлене якимись чинниками. Зауважимо, що наведені числа відносяться до номінальних, а не кількісних, через те, що результатом одиничного спостереження є факт народження хлопчика або дівчинки, а не якесь число. Наведені ж числа є частотами двох альтернативних подій.

Згрупуємо дані у таблицю:

Така таблиця (без стовпчика "різниця") називається таблицею спряженості категорій. В даному випадку категорій дві, але таблиці спряженості можуть бути і більшими.

Отже, чи є різниця в 3% між реальним життям і теорією випадковою? Для відповіді на це питання існують критерії узгодженості, найбільш поширеним з яких є критерій узгодженості χ² Пірсона (читається "хі-квадрат"). Статистика цього критерію обчислюється за формулою:

де χ² - статистика тесту, О_i - число спостережень типу і або емпіричні, експериментальні дані (О від observations), E_i - очікуване у відповідності до теорії число спостережень типу і (Е - expectations), n - число комірок таблиці.

При нульовій гіпотезі ()про узгодженість між експериментальними даними і теорією) значення очікуваних та спостережених частот є однаковими, а χ²=0. Чим значення статистики критерію є більшим, тим меншою є ймовірність, що різниця випадкова. За χ² обчислюється величина р, на основі якої ми приймаємо рішення, відкидати чи приймати нульову гіпотезу.

Для наших даних χ² = 257.9, а р = 0 (насправді, не точно 0, а 3*10^-114). Таким чином, ми повинні відкинути нульову гіпотезу і визнати, що хлопчиків народжується з певних причин більше, ніж 50%. Дійсно, біологічні особливості процесів запліднення та внутрішньоутробного розвитку людини такі, що на 106 хлопчиків народжується 100 дівчаток.

Тест χ² часто використовується в генетиці, коли нам потрібно оцінити, чи узгоджується спостережене розщеплення при схрещуванні різних організмів із теорією, визначеною законами Менделя (або іншими закономірностями успадкування). Приміром, у відповідності до третього закону Менделя при схрещуванні гетерозиготних за двома ознаками організмів (нехай це буде класичний горох із жовтим гладеньким насінням) ми повинні спостерігати розщеплення 9:3:3:1 (жовті гладенькі - жовті зморшкуваті - зелені гладенькі - зелені зморшкуваті відповідно). Провівши таке схрещування і порахувавши кількість рослин з різними комбінаціями ознак у наступному поколінні, ми отримали такі результати:

В нижньому рядку наведено очікуваний розподіл, який був розрахований як пропорції 9/16, 3/16 та 1/16 (16=9+3+3+1) від суми усіх емпіричних даних. Обчислене значення χ² становить 1.26, а визначене р = 0.18. Отже, ми не можемо відкинути нульову гіпотезу і визнаємо емпіричний розподіл еквівалентним теоретичному 9:3:3:1. Іншими словами, ми визнаємо, що відхилення між спостереженням та теорією є випадковим.

Зауважимо, що для таблиць 2х2 як у прикладі з народжуваністю, статистику χ² потрібно обчислювати за дещо відмінним алгоритмом - з поправкою Йейтса на неперевність даних. Більшість статистичних програм мають можливість обрати між двома варіантами - χ² та χ² з поправкою (Yates correction, correction for continuity).

У випадку, якщо кількість спостережень однієї з категорій (або ж теоретичне значення частоти) є меншою за 10, χ² навіть з поправкою погано вирішує поставлену задачу. В такому випадку слід використовувати тест Фішера (точний тест Фішера, Fisher's exact test, не плутати з F-тестом для порівняння дисперсій, який також є тестом Фішера).

В LibreOffice обчислення χ² здійснюється функцією CHISQ.TEST або CHITEST, аргументами якої є два ряди даних з частотами розподілів, а результатом - обчислене р. Слід звернути увагу, що ця процедура не враховує поправку Йейтса для таблиць 2х2.

В пакеті PSPP є опція "Аналіз" - "Непараметричні критерії" - "χ квадрат". На відміну від LibreOffice та розглянутих вище приладів вона працює не з частотами категорій, а з сирими даними - змінними, які містять інформацію про окремі виміри. В якості теоретичних частот можна зазначити дефолтний варіант "частоти усіх категорій рівні" або ввести свої розрахунки.

Обчислити χ² можна і онлайн, наприклад, за посиланням http://www.quantpsy.org/chisq/chisq.htm

Алгоритм цього сайту враховує і поправку Йейтса.

Також, існують онлайн версії і тесту Фішера: http://www.langsrud.com/stat/fisher.htm

Зважаючи, що невеликі таблиці 2х2 складаються всього з чотирьох значень, в даному випадку використання онлайн ресурсів є досить зручним.